ここで α は微細構造定数である。 また、 リュードベリ定数 R ∞ と微細構造定数 α により a 0 = α 4 π R ∞ {\displaystyle a_{0}={\frac {\alpha }{4\pi R_{\infty }}}}27/9/18 数学 『アティヤの発表によると微細構造定数を導出したとのこと。 リーマン予想はボーナス。 個人的には微細構造定数の方が重要。 本当ならば軽くノーベル賞クラス』 Togetter 『アティヤの発表によると微細構造定数を導出したとのこと。 リーマン核生成と界面 京都大学・工・材料工学 西谷滋人∗ 平成15 年12 月11 日 概要 凝固現象は熱伝導度や溶質分配などのバルクの物性によってその主要な点の多くは理解で

リーマン予想
微細構造定数 導出
微細構造定数 導出-大学院「先進構造材料特論」 04 10年度 担当:辻 4.超微細結晶粒金属材料 (1) 金属材料の強化原理 Table 31 材料の強化機構 加工硬化(転位強化) 加工によって転位密度を高める 結晶粒微細化強化 結晶粒を微細化するであり、微細構造定数αは、 α= e2 4 πε0 hc = 1 137 (10) から j ψ(0)j2 / e6 / α 3 (11) である。 また、 σ2 γ/ e 4 / α 2 (12) であることから、式(7) を計算するとパラポジトロニウムの寿命は τ2 γ= 2 m α5 = (123ps) (13) と求められる。 図2 パラポジトロニウムの
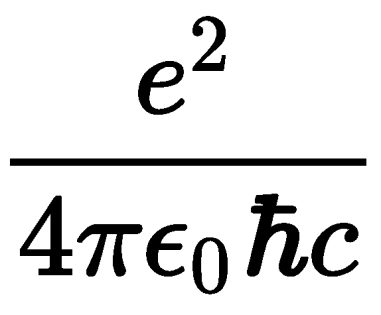



ネギトロ量子論 微細構造定数と蠱毒と世界 オモコロブロス
α= 微細構造定数≈ 1 137 me = 電子の質量 c= 光速 (25) である 可能な観測値はα,β= ±1, 相関関数は αβ = −κcos2ϕとする まず, A,B 地点での観 測値が(α,β) となる確率pαβ(ϕ) を考えるために, 以下の条件を5 522 析出強化(precipitation strengthening) 図58 AlCu系合金の溶体化処理と時効 図59 オロワン機構の説明図 溶体化処理により過飽和固溶体を生ここで、静磁場に垂直に!~ で回転する磁場h~1 を加えることを考える。 この場合、(3) において静磁場h~0 をh~ 0 h~1 で置き換えた式が成立する。 ところがh~1 と共に回転する座標系ではh~0、h~1 両方とも静止して 見える。回転系のz 軸をh~0 方向に、x 軸をh~1 方向にとる。 ここで、実験室系で
0㷈c = 1/は微細構造定数で、Sommerfeldが 1916年に分光学の立場で導入。電磁相互作用の強さを表わす。 Niels Bohr、 デンマーク、 Arthur Compton 米、 Arnold Sommerfeld, ドイツ、 mec2=自己電磁相互作用 エネルギー=e2/4πε 0re 不確定性 関係水素原子の線スペクトルを表す物理定数であり、 で与えられる。ここで と はそれぞれ電子の質量と電荷、 は真空中の光速、はプランク定数、 は真空の誘電率である。この式は、微細構造定数 を用いると と書くことができ、cgsガウス単位系では となトキー放出型電子銃の構造、電界解析に使用した表面 電荷法の概略を説明し、解析結果について述べる。 2 ショットキー放出 ZrO/W陰極内部の電子密度分布と陰極表面近くの電 位障壁を図1 に示す。電位障壁は「鏡像電荷」と「外 部電界」によって決まる。
重力定数 G 667 10 8 dyn cm2 g 2 G M 1L3T 2 微細構造定数 e= e2= hc (CGS)= q2=4ˇ 0 hc (SI) 1/(137 102) = 730 10 3 重力微細構造定数 g = Gm2 p= hc 590 10 39 アヴォガドロ数 N 602 1023 mol 1 ボルツマン定数 k 138 10 16 erg K 1 = 862 10 5 eV K 1 ボーア磁子 B = e h= 2me 927 10 21 gauss cm3 2 長さ cm pc light year AUM uはモル質量定数です(定義により1 g / mol) αは微細構造定数です。 寸法式:M1T3Θ4 関連する定数は放射定数 (または放射密度定数 ) aです。微細構造、超微細構造、ゼーマン効果(Zeeman Effect) 水素原子には、主量子数n以外に、微細構造、超微細構造と呼ばれるエネルギー準位の分裂があるようです。 微細構造(Fine Structure) 微細構造を含む水素原子のエネルギー準位図です。




微細構造定数 Wikiwand



スピン軌道微細構造のエネルギー計算
のように求められる。微細構造定数α は、 α e2 4π†0~c (43) であるので、トムソン散乱断面積は微細構造定数を用いると、 σT = 8π 3 µ e2 4π†0~c ¶2 ~2 m2 ec2 = 8πα2~2 3m2c2 (44) のようにも表せる。 14 トムソン散乱(入射光が無偏光の場合)微細構造の近似形の導出。 (Eq1) ディラックの水素 = ボーア・ゾンマーフェルト模型。 このサイト や このサイト (p12) にあるように、ボーア・ゾンマーフェルト模型は ディラックの水素と まったく 同じ 微細構造のエネルギー値を与える。 微細構造定数 導出 微細構造定数はネイピア数e円周率π電気定数ε光速c等で構成されてるわけだから これらの定数も影響を受け得ると考えるのは自然な流れだろう とまぁアティヤがそう述べてるわけで 900ご冗談でしょう名無しさん



Asahi Net Or Jp




リーマン予想
Mec 2 は電子の静止質量である。 光電効 果の断面積は物質の原子番号 Zの5乗に比例し,!OPsとpPsの間には電子, 陽電子間の磁気モーメントの相互作用の差異によって生じるエネルギー差が存在 し, それは3GHz(084meV) である(oPs の方がエネルギーが高い*1) これは超微細分裂(HFS;HyperFine Splitting) と呼ばれている*2 113 ポジトロニウムの崩壊 前述のようにポジトロニウムは有限の寿命を2原子分子 (直線分子) 分子ガスの最も基本的なトレーサー 同位体分子 (isotopologue) 13C16O, 12C18O などもよく観測される 回転は分子軸に垂直なものだけが可能 ひとつの量子数 J(=0, 1, 2, ) で表される E rot=hBJ(J1) B=h/(8"2I) rotational constant s‒1 ν(J=1–0) = 2B = GHz (26 mm) 双極子モーメントは小さい (01 debye) 存在度が大きい (X CO~104) ために強いス ペクトル



2



微細構造定数137というのはどういう部分が興味深いのでしょうか Quora
微細構造定数の存在は、プランク定数と光速度が 1 の単位系を選択したら、その単位系での素電荷の値が決まってしまうことを意味します。 「プランク定数と光速度の二つだけでは長さ・質量・時間の三つの基本単位の組み合わせには自由度 1 が残っている。運動に由来するスペクトルを中心にして,そこから物質の構造,性質を理解す ることを学ぶ。光と物質の相互作用を通して,物質の構造や化学現象を研究す る学問分野のことを,分子分光学という。 13 12 スケジュール 13 参考書改定si では磁気定数 μ 0(および電気定数 ϵ 0)は定 義量でなくなり不確かさを持つ被測定量である。そ の不確かさは、微細構造定数 α、真空の特性インピー ダンス z 0、真空の特性アドミッタンス y 0 と同じ(改 定時点で拡張相対不確かさ 23 × 10–10)で



微細構造定数137というのはどういう部分が興味深いのでしょうか Quora




最速 リーマン予想 証明 アティヤ
水素原子の微細構造の理論的 説明は1916 年にSommerfeld 12 が前期量子論の手法によって行った。この時に微細構造定数が導 入されている。どの微細構造の説明のために相対論的な量子力学を構築する動きがあった。例えば、に基づく物理定数の要約を示す。 詳細は Fundamental Physical Constants from NIST を参照されたい。 19年5月日に施行された SI 基本単位の再定義により 単位と物理定数の定義構造は大きく変更さ超微細相互作用弱いといと予測予測されㄩㄩㄩㄩ大大きなきなbbbbwww効暍効暍がが晓待晓待されるされるㄦ ㄦㄦㄦ 原子分光学的手法による 不安定同位体bebeののの核構造研究核構造研究 (2) 777be ( iiii= 3/2)),, ), 半減晓), 半減晓旍旍




科学理論について
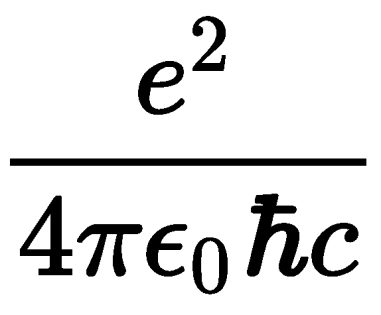



ネギトロ量子論 微細構造定数と蠱毒と世界 オモコロブロス
比例定数を与えると (付録参照)、それに対応して微細構造定数も定義されるが、 その数値は二つの単位系で同じになる。これは微細構造定数 αが無次元量である から当然である。 2 30 8 6 6 10 kg 10 m/s 10 eV 05 10 eV mc = × × × − = × ×となる.ここで,α=e2/(¯hc)は微細構造定数(finestructureconstant)である.また,長さ の単位として1fm=10−15 m ()()は = 1と書ける.ただし,上式中のaは(13)の微細構造定数ではなく,a=(4/9p) 1/3 と定義される.クォークの命名者もかつてはこのようないささか泥臭い計算に従事したという事実は記憶に留めてよいだろう.上の(16)式にはr s ln r s という対数的な特異性を示す項が含まれているが,これは電子ガスの




ラムシフト Wikipedia




1769号 微細構造の解析方法 装置およびプログラム Astamuse
原子の電子配位による多重項のスペクトル線を詳しく みると,そ れぞれのスペクトル線はさらにいくつかの成 分に分離されるこ の微細な分離が超微細構造(hfs hyperfine structure)と 呼ぼれているこ れが,原 子中 心にある原子核による効果であることは,今 から50年 以上も前に確立している1)原子核とそれを取り巻く電 子(原 子電子)と の電磁相互作用の結果であったあいだの距離である。また,α は微細構造定数 (fine structure constant)と呼ばれる無次元の 量で,SI単位で,真空の誘電率をε 0 として α = e2 4πε 0¯hc ≈ 1 137 (172) である。このような原子を水素様原子,あるい は水素型原子(hydrogenlike atom)という。 r V( )r 0微細構造定数α= を決定する新しい方法となるこ とを提案した。この実験ではゲート電圧を変えることに より電子濃度を変化させている。またホール電圧と電流 の比からホール抵抗を求めることができる。 図3 ホール効果 図4 mosfet




クッパ姫騒ぎの最中に 理系界に走った衝撃をまとめました 160年間未解決で 証明すると1億円貰える問題である リーマン予想の証明が発表された 証明は歳の数学者アティヤさん 論文がたったの5ページで完結 他の研究の おまけ として証明された



素粒子の内部構造 仮想光子 ダークマター ダークエネルギーと真空エネルギー 黄金数とフィボナッチ数列
この電子の速度の 光速 (c) に対する比が 微細構造定数 α になる。 ( 別の方法による微細構造定数の導出 = Eq23 ) Eq21 より、φ がゼロのとき、 σ、v、β は次のようになる。 (Eq24) 近日点では 速度は 接線方向である。 微細構造定数は、ネイピア数e、円周率π、電気定数ε、光速c等で構成されてるわけだから、 これらの「定数」も影響を受け得る、と考えるのは自然な流れだろう。 と、まぁ、アティヤがそう述べてるわけで。 900ご冗談でしょう?E" の35乗に反比例する. 332 コンプトン効果 (Compton Effect) γ線が(自由)電子により弾性散乱される現象で ある。 電子の束縛エネルギーを無視する




聖書gematoria パウリ ファインマン ゾンマーフェルトと超微細構造定数137 Blogchemistry




微細構造定数 しろグ
アボガドロ定数NAを測定→ プランク定数h を導出 キッブルバランス法(米国、カナダ、フランス、スイス、中国、韓国) 電気的手法によってプランク定数h を測定 e A 2 e e 2 McM m R h N c :真空中の光速度 :微細構造定数 R :リュードベリ定数 3/1042 粒界強化(結晶粒微細化強化) 一般の金属材料は複数の結晶粒から成る多結晶である.この金属材料を強化するためには,塑性変形 を担う転位のすべりを抑制する必要がある.(すべりに要する応力を増大させる)その強化方法には,超微細構造を持つ原子にレーザー光をあて、微細構造準位間の電気双極子遷移をおこさ せる場合、起こりうる遷移の選択則は、DJ = 0,±1 かつ DF = 0,±1 (ただし、 J g = 0 → J e =0とF g = 0 → F e =0のときは、禁止遷移)である。 22 スペクトルの幅




微細構造 原子物理学 Wikipedia




真空微細構造定数 新しい理論
電子の分散関係(43) から、エネルギー状態密度を導出する。まず、エネルギーがE より 低い状態の数をN(E) とおく。(43) 式より、波数空間で半径k = p 2mE ℏ の球の内側の状 態を数えれば、N(E) になる。そこで、(47) 式をjkj< p 2mE ℏ




最速 リーマン予想 証明 アティヤ




理研など 基礎物理定数 微細構造定数a を40億分の1の精度で決定 Tech



壁紙hdについての最良の選択 立派な 微細構造定数 導出



アティヤの発表によると微細構造定数を導出したとのこと リーマン予想はボーナス 個人的には微細構造定数の方が重要 本当ならば軽くノーベル賞クラス Togetter



微細構造定数 異常磁気能率




物理専攻しか解けない 物理定数クイズ



微細構造定数 異常磁気能率



微細構造定数に関連する2件のまとめ Togetter



2



2




壁紙hdについての最良の選択 立派な 微細構造定数 導出




微細構造定数近似式 自作式 サガリバナのため息 植物や微細構造定数の近似式等



放射線概論という本を読んでいてあまり物理学には詳しくないのですが Yahoo 知恵袋
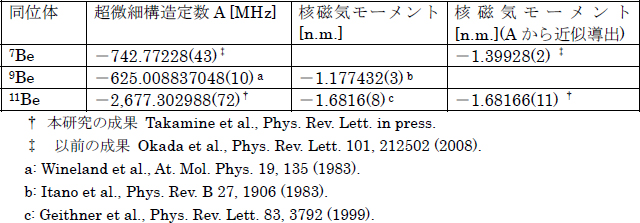



中性子ハロー核11beの超微細構造定数の精密測定 理化学研究所




オイラー積 サガリバナのため息 植物や微細構造定数の近似式等




ネギトロ量子論 微細構造定数と蠱毒と世界 オモコロブロス
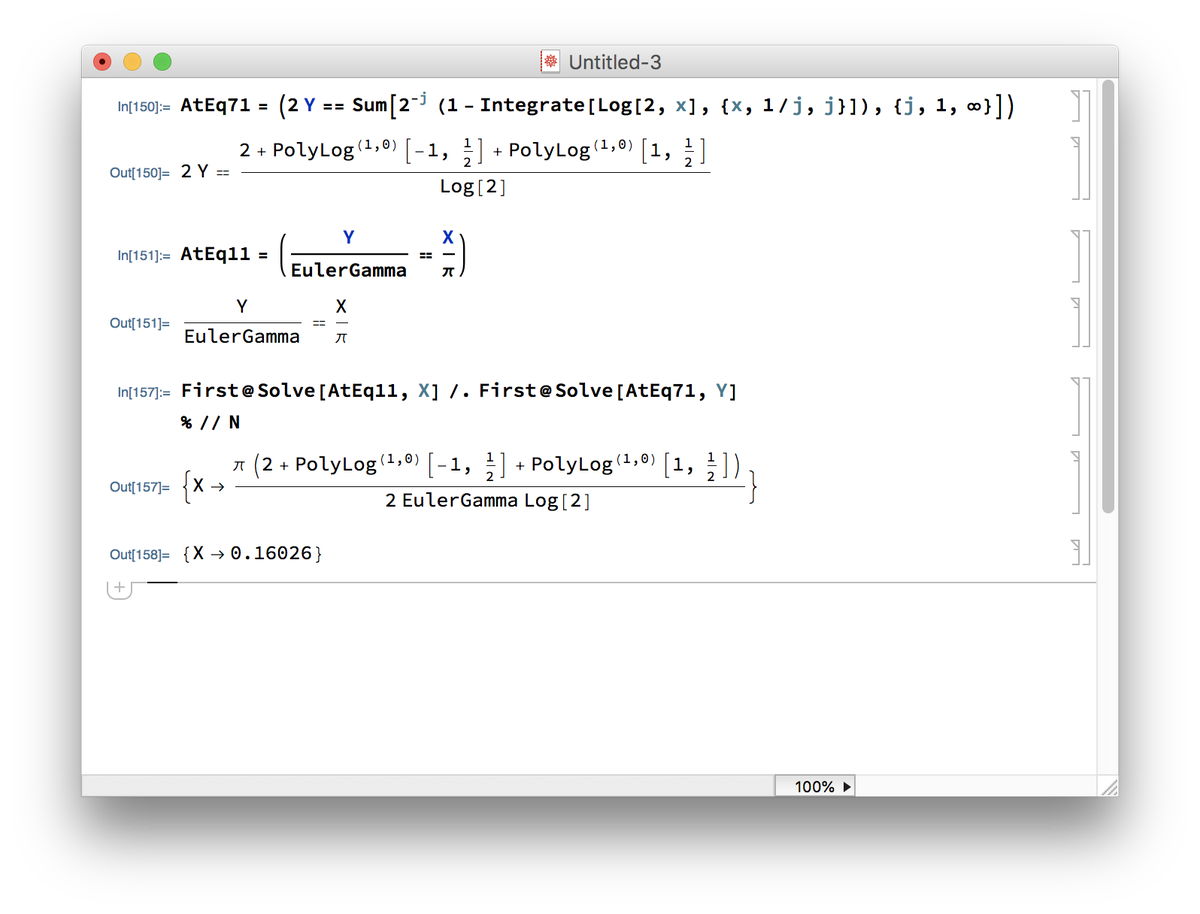



アティヤの発表によると微細構造定数を導出したとのこと リーマン予想はボーナス 個人的には微細構造定数の方が重要 本当ならば軽くノーベル賞クラス Togetter



2



微細構造定数137というのはどういう部分が興味深いのでしょうか Quora



微細構造定数について 説明できる方いませんか 量子力学に出てくるある Yahoo 知恵袋



微細構造定数 異常磁気能率




Yuya U Atiyahの微細構造定数の導出の中で 多重ベルヌーイ数が必要のようだが K J が巨大な数になるから 計算できない気がするんだが リーマン予想




真空微細構造定数 新しい理論




理研など 基礎物理定数 微細構造定数a を40億分の1の精度で決定 Tech




超微細構造 Wikipedia




理研など 基礎物理定数 微細構造定数a を40億分の1の精度で決定 Tech




ネギトロ量子論 微細構造定数と蠱毒と世界 オモコロブロス




壁紙hdについての最良の選択 立派な 微細構造定数 導出
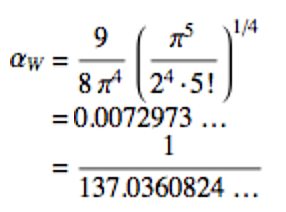



壁紙hdについての最良の選択 立派な 微細構造定数 導出



2




1769号 微細構造の解析方法 装置およびプログラム Astamuse



微細構造定数ってなに ぽこにっき



2



微細構造定数 異常磁気能率




微細構造 原子物理学 Wikipedia




壁紙hdについての最良の選択 立派な 微細構造定数 導出




微細構造定数とリーマン予想と物理学帝国主義 Biophysical Psychiatry
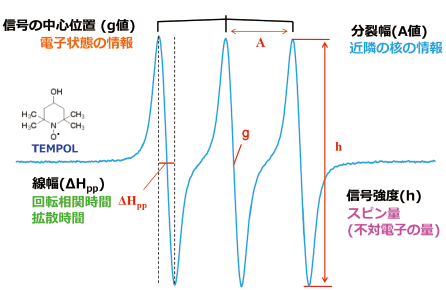



電子スピン共鳴装置 Esr の原理と応用 Jaima 一般社団法人 日本分析機器工業会



2




壁紙hdについての最良の選択 立派な 微細構造定数 導出




ネギトロ量子論 微細構造定数と蠱毒と世界 オモコロブロス




科学理論について



微細構造定数 異常磁気能率
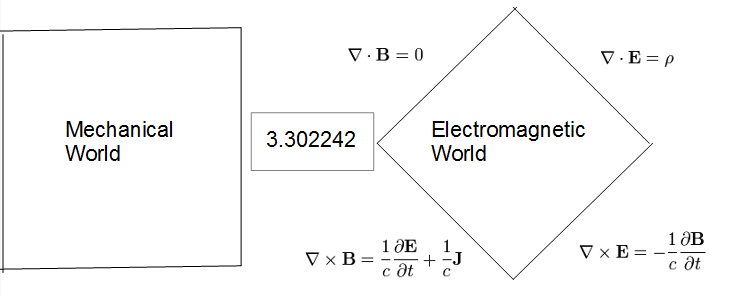



E0 M0の秘密 自然単位系からの Si 単位系の考察 Jpn




微細構造定数近似式 自作式 サガリバナのため息 植物や微細構造定数の近似式等




微細構造定数と 意味ある偶然の一致 新muのブログ




微細構造定数と 意味ある偶然の一致 新muのブログ



壁紙hdについての最良の選択 立派な 微細構造定数 導出




3大望遠鏡で挑む 100 億年前の宇宙の自然法則 観測成果 すばる望遠鏡




物理定数は変化する 日経サイエンス




ついにリーマン予想が証明された とね日記



アティヤの微細構造定数を計算したという論文のメモ Velocitymatrix15 S Blog



微細構造定数137というのはどういう部分が興味深いのでしょうか Quora



2
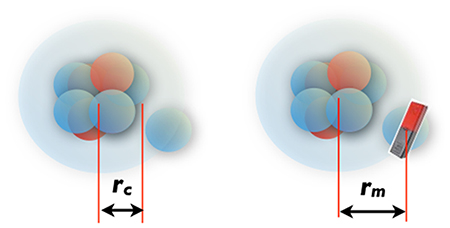



中性子ハロー核11beの超微細構造定数の精密測定 理化学研究所
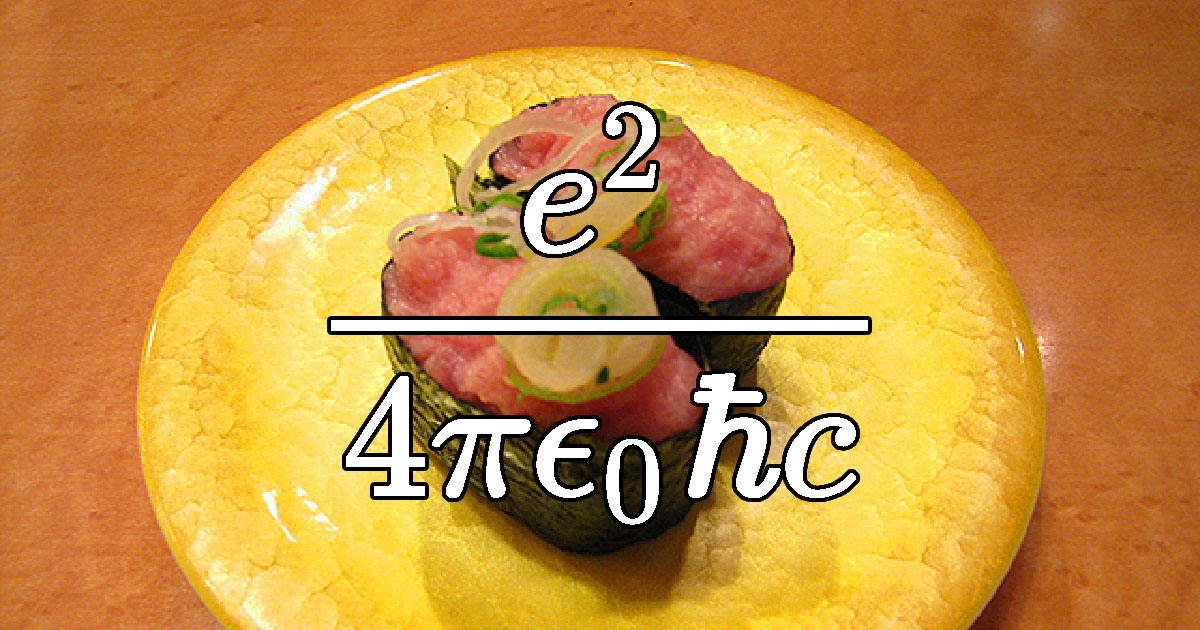



ネギトロ量子論 微細構造定数と蠱毒と世界 オモコロブロス




3大望遠鏡で挑む 100 億年前の宇宙の自然法則 観測成果 すばる望遠鏡



2
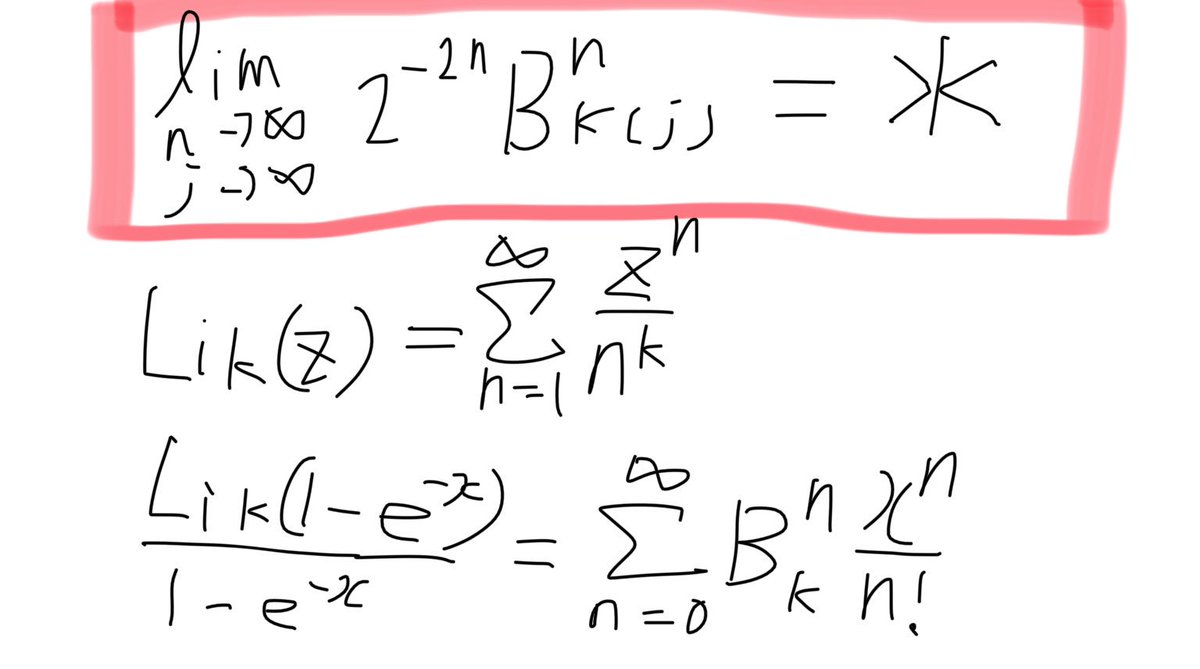



Yuya U Atiyahの微細構造定数の導出の中で 多重ベルヌーイ数が必要のようだが K J が巨大な数になるから 計算できない気がするんだが リーマン予想



アティヤの発表によると微細構造定数を導出したとのこと リーマン予想はボーナス 個人的には微細構造定数の方が重要 本当ならば軽くノーベル賞クラス Togetter




アティヤの発表によると微細構造定数を導出したとのこと リーマン予想はボーナス 個人的には微細構造定数の方が重要 本当ならば軽くノーベル賞クラス Togetter




微細構造定数




物理学が好きな時雨 ところで 素数の並び方はきわめてランダムだよね 2 3 5 7 11 13 17 しばらく続く領域もあれば ずーっと合成数が続く領域もある つまり リーマン予想は素数の分布についての結果を含んでいる




理研など 基礎物理定数 微細構造定数a を40億分の1の精度で決定 Tech



微細構造定数の値を計算しておこう T Nakaの阿房ブログ
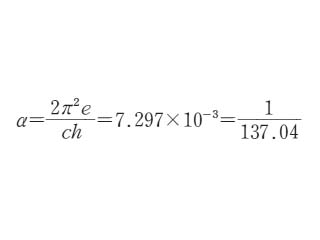



ゾンマーフェルトの微細構造定数とは コトバンク




X Seek アティヤの発表によると微細構造定数を導出したとのこと リーマン予想はボーナス 個人的には微細構造定数の方が重要 本当ならば軽くノーベル賞クラス



2



微細構造定数の導出で なんでひゃまの回答がbaじゃないねんhttp Yahoo 知恵袋
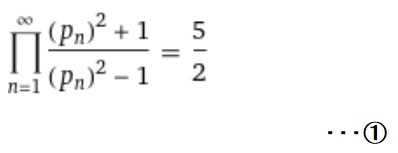



オイラー積 サガリバナのため息 植物や微細構造定数の近似式等




微細構造定数とは Satohakase Note
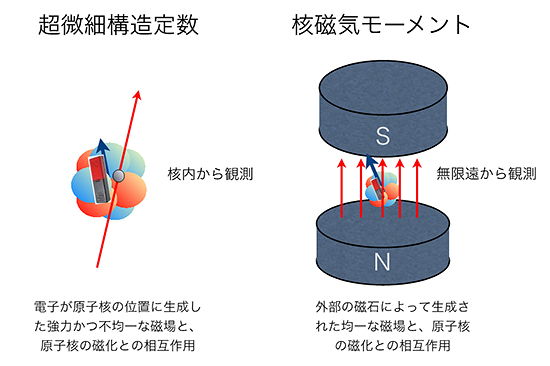



中性子ハロー核11beの超微細構造定数の精密測定 理化学研究所
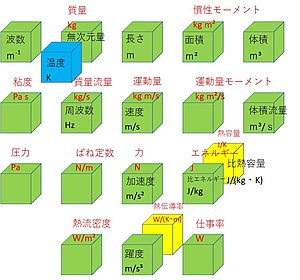



量の次元 Wikipedia




15 号 液体処理装置及び液体処理方法 ならびにプラズマ処理液 Astamuse




宇宙の法則は乱れない 超大質量ブラックホールの近くでも基礎物理定数は変わらなかった ニコニコニュース



微細構造定数 異常磁気能率



Ils Uec Ac Jp




Masahiro Hotta またプランク定数ℏを今度は10の70乗大きくして あるマクロな時間を経過させた後に 再び元の小さな値に戻るとしよう すると今度は量子重力の実験が可能になる プランク長さは10のマイナス35メートル程度だが ℏが大きい間にそれはメートル



理研など 基礎物理定数 微細構造定数a を40億分の1の精度で決定 Tech
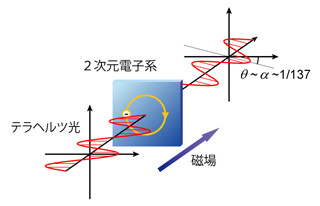



理研など 基礎物理定数 微細構造定数a を40億分の1の精度で決定 Tech




微細構造 原子物理学 Wikipedia




微細構造定数 137とパウリ ユング 真実を求めて go go



0 件のコメント:
コメントを投稿